How to Break Your Random Network Distillation
How to Break Your Random Network Distillation
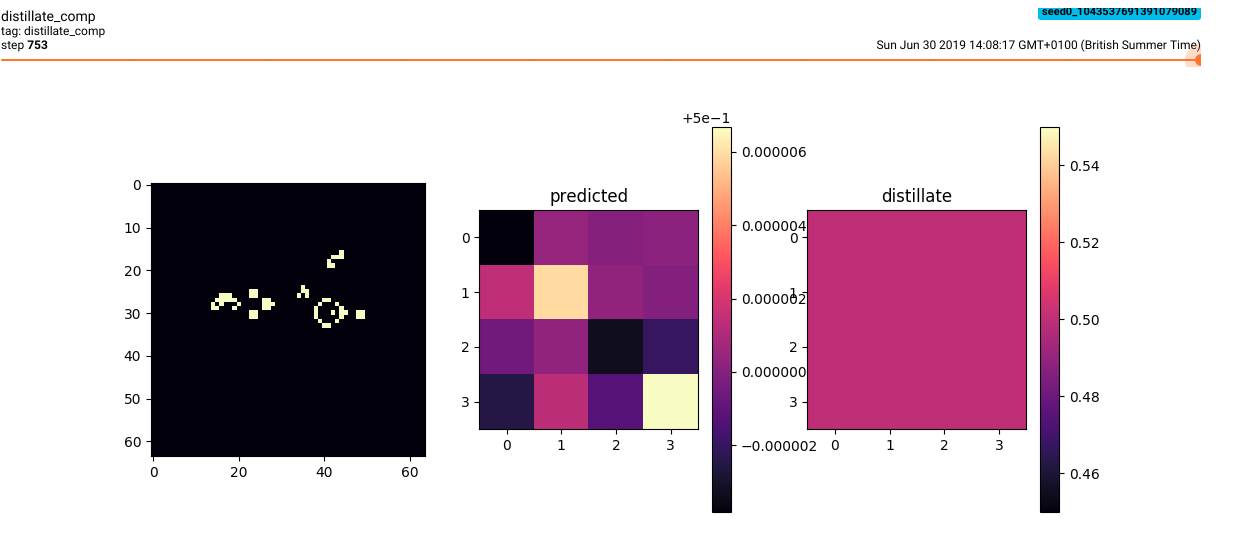
TL:DR To be capable of curiosity-driven exploration, an agent must be capable of being surprised. In one failure mode, shown above, a random transformation is easy to learn because the values are always essentially 0.5.
The Problem
The field of reinforcement learning has made great strides by incorporating deep learning neural nets, and yet RL famously doesn’t really work for most problems. One challenge holding RL back from having real-world impacts is reward shaping, with sparse rewards being particularly difficult to deal with. As you may know from personal experience, motivation and planning become more difficult with sporadic, sparse, and ambiguous rewards. It’s comparatively easy to reinforce a new chess strategy after a successful match, and much more difficult to determine just what it was about your 10th self-published novel that caused the audience to finally bloom beyond your immediate friends and family. RL agents, humans, and pigeons in a Skinner box all have similar difficulties parsing rewards into effective strategies for future scenarios.
Rather than starting from real-world scenarios and devising training algorithms capable of general intelligence from the beginning, the art of RL experimentation is in large part a matter of finding problems that are close to what known RL strategies can solve. Some heuristics denoting good candidates for RL problems include:
- It should be plausible for an agent acting randomly to stumble upon rewards at every point of the learning curve.
- Rewards and environmental state-changes can’t be too stochastic.
- The problem can be approximated in simplified or modular ways. This helps to build related toy problems to determine if the larger problem may be tractable, e.g. it might be useful to use position vectors as inputs before saddling the RL agent with the task of learning vision from scratch.
A good reference for more useful guidelines to approaching problems from an RL perspective is John Schulmann’s Nuts and Bolts of Deep RL Experimentation
Most RL agents learn through some form of trial-and-error, but naively this approach can take forever. Adjusting the trade-off between exploitation of learned strategies and exploration of action consequences is a central part of solving even moderately complicated RL problems. A simple way to do this is to have a parameter like ‘temperature’ with hotter temperatures increasing the likelihood of sampling less-likely actions.
Improved exploration strategies involve some form of uncertainty estimation or proxy. To improve sample efficiency, it makes sense to encourage RL agents to learn to be curious by encouraging an agent to seek out unfamiliar states. One of these ways is called random network distillation, where the inability of a model to predict a fixed random transformation of the current state generates higher rewards. Notably, random network distillation is not susceptible to the “Noisy TV problem,”that plagues next-state prediction, where an RL agent becomes addicted to stochastic state changes. In this essay we will tinker with great ways to make random network distillation a total waste of effort.
The Environment: Conway’s Game of Life
Conway’s Game of Life is a famous example of a cellular automaton (CA) universe. A 2D grid of cells all possess a binary state, either 1 or 0, and the universe evolves by discrete time steps where each cell’s state at the next time step depends on its own state as well as the sum of states of its 8 neighbors. For this particular CA, the rules determine that an active cell with 2 or 3 immediately adjacent neighbors will remain in state 1, while a cell in state 0 will become 1 if it has exactly 3 neighbors. Cells in any other situation will stay or transition to 0 in the next time step. In the ‘S/B’ syntax of the “Life” family of CA rules, Conway’s game of life is defined by its rules ‘S23/B3’ where the ‘S’ and the ‘B’ in the ‘S/B’ format are named for survival and birth, respectively, in keeping with the theme of a CA universe designed to mimic some of the characteristics of living systems.
How to break your RND
OpenAI used random network distillation to be one of the first (concurrent with an ICLR submission from Choi et al) to beat average human performance on Montezuma’s revenge, without using imitation learning. Montezuma’s revenge is the most notorious of the ‘RL-hard’ Atari games, a list of games that also includes Solaris, Venture, Gravitar, Freewary, Private Eye, and Pitfall! (Bellemare et al. 2016). As noted in the blog post, RND isn’t a magic wand and it must be balanced and bug-free to yield the state-of-the-art results demonstrated in the paper. We’re going to do the opposite, and see if we can figure out just what is the best way to break your RND.
Strategy 1: predictor learns universal physics instead of curiosity
The next state of any given cell in a CA universe is fully determined by the state of its immediately adjacent neighbors in a 3x3 grid. Consequently it’s not surprising that using conv-nets with 3x3 convolution kernels for both random transformation and to learn said transformation is a recipe for a very non-curious bot. With both the random network and the predictor producing spatially invariant outputs, a novel scene will continue to generate the same reward signal so long as the rules remain unchanged.
Strategy 2: bad random initialization
Another failure mode for random network distillation occurs from bad initialization. With a random network poorly initialized with small weight values very close to 0 and a sigmoid activated output, output values will all fall very close to 0.5 (falling around 0.0 without the activation). Therefore the weights need to be initialized in a way that produces interesting results with a wider range or else the prediction network can minimize its loss function by simply learning the average value.
Strategy 3: non-static random networks
This last method for breaking RND is matter of code hygiene rather than a strategic mistake. Early on in this project I had a bug in my code that led to the random network being reset each episode, which led to a boost in rewards as the prediction network had to re-learn the (new) transformation each time. There’s nothing clever about fixing this problem by using a static seed, but it’s a good reminder that writing bug-free code can be make-or-break when building new implementations.
Un-breaking your RND
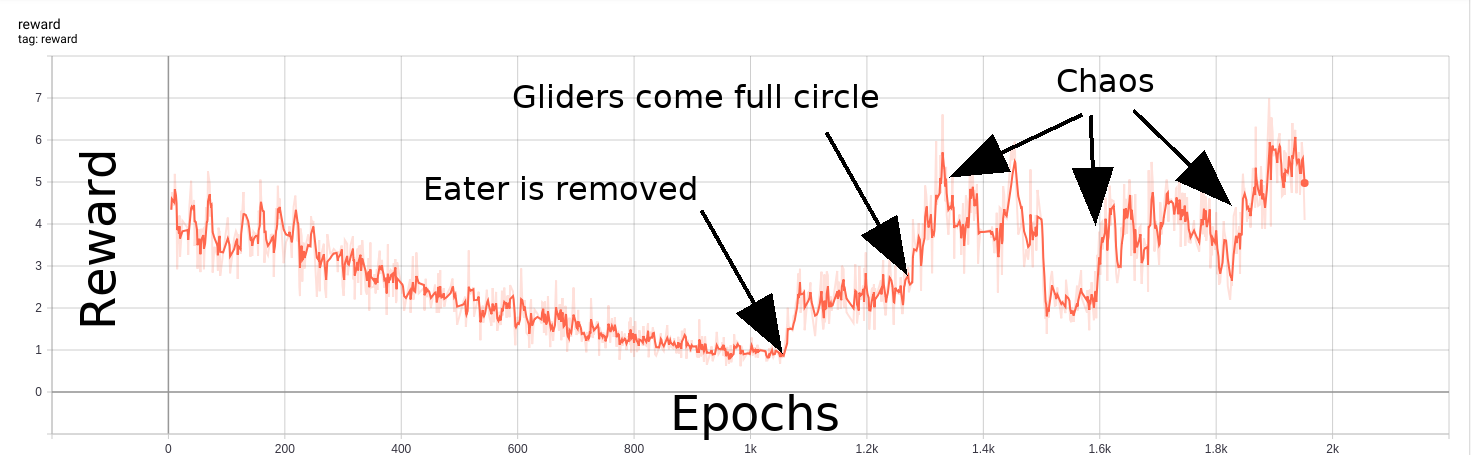
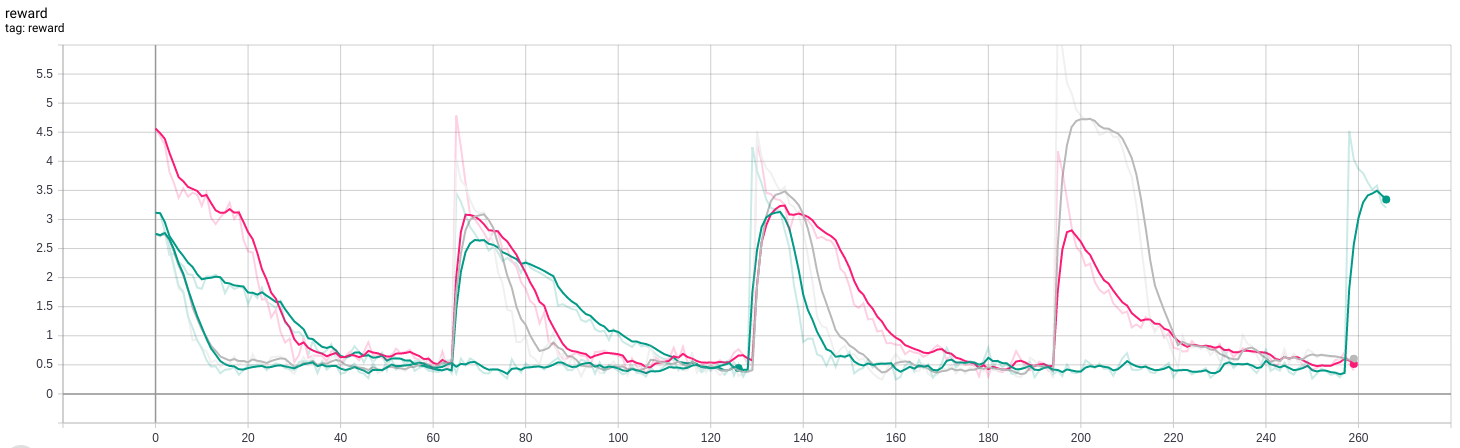
With good initialization, dense layers in the random network, and obvious bugs eliminated, it was possible to generate an effective curiosity-based reward. In this example, I built a Gosper glider gun, an oscillating pattern that continuously produces small gliders. I used a fishhook eater to annihilate the gliders, yielding a stable oscillator that repeats every 30 steps. After sufficient training steps for the predictor to learn the random network distillate for this scenario, the fishhook is removed. Shortly thereafter, wrap-around gliders lead to machine destruction and general chaos that the RL agent finds quite exciting.
This experiment was an action-free exploration of random network distillation, that is, the RL agent was prevented from making any changes to the CA universe. Conway’s Game of Life and similar CA rulesets could provide a fertile playground for studying creative collaborations between humans and machines. If RL agents can amplify the ability of a human CA enthusiast to discover and design cool machines in the simplified world of 2D cellular automata, that’s a reasonable stepping stone to building cool machines in the real world. I’m working on this project here.
References:
Yuri Burda, Harrison Edwards, Amos Storkey, Oleg Klimov. Exploration by Random Network Distillation. Arxiv.org. 1810.12894. 2018 October. OpenAI Blog post
Jongwook Choi et al.Contingency-Aware Exploration in Reinforcement Learning International Conference on Learning Representations. 2019.
Bellemare et al.Unifying Count-Based Exploration and Intrinsic Motivation 30th Conf. on Neural Information Processing Systems. (2016).